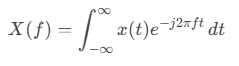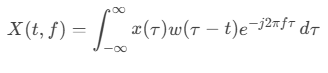Fundamentos Matemáticos: De la Transformada de Fourier a la STFT

Transformada de Fourier Continua (FT)

La Transformada de Fourier (FT) de una señal continua x(t) se define como:

Esta representación indica qué frecuencias están presentes en la señal, pero no cuándo ocurren. Para señales estacionarias (cuyas propiedades no cambian en el tiempo), la FT es suficiente. Sin embargo, el audio es una señal no estacionaria, por lo que se requiere un enfoque diferente.

Transformada de Fourier de Tiempo Corto (STFT)

La STFT introduce una ventana deslizante $w(t)$ que aísla segmentos temporales de la señal antes de aplicar la FT. Matemáticamente:

Donde:

• w(t) es una función de ventana (e.g., Hann, Hamming, Blackman).
• t es el instante de tiempo analizado.
• f es la frecuencia.

La STFT produce una representación tiempo-frecuencia que puede visualizarse mediante un espectrograma.

Parámetros Clave en la STFT

La calidad y resolución de la STFT dependen de:

• Tamaño de la ventana ($N$):
  • Ventanas largas → Mayor resolución en frecuencia, menor resolución temporal.
  • Ventanas cortas → Mayor resolución temporal, menor resolución en frecuencia (Principio de Incertidumbre de Heisenberg-Gabor).
• Solapamiento (Overlap):
  • Para evitar pérdida de información, se suele usar un solapamiento del 50%-75%.
• Tipo de Ventana:
  • Rectangular: Simple pero con altos lóbulos laterales (leakage).
  • Hann/Hamming: Reduce el leakage, mejor para análisis espectral.

Espectrograma: Visualización del Dominio Tiempo-Frecuencia

Un espectrograma es una representación gráfica de la magnitud de la STFT ($|X(t,f)|$):

• Eje X: Tiempo.
• Eje Y: Frecuencia.
• Color/Intensidad: Energía (dB) o magnitud.

Ejemplo de un espectrograma de una señal de voz:

• Formantes: Bandas de alta energía correspondientes a las frecuencias resonantes del tracto vocal.
• Armónicos: Componentes periódicos en señales de instrumentos musicales.

Tipos de Espectrogramas

• Espectrograma de Amplitud: Muestra $|X(t,f)|$.
• Espectrograma de Potencia: Muestra ∣X(t,f)∣2∣X(t,f)∣2.
• Espectrograma en Escala Logarítmica: Útil para audio, ya que el oído humano percibe frecuencias logarítmicamente (e.g., escala Mel).

Aplicaciones en Procesamiento de Audio

Compresión de Audio (e.g., MP3, AAC)

• Se usa la STFT para identificar componentes irrelevantes (enmascaramiento auditivo) y comprimir selectivamente.

Reconocimiento de Voz y Música

• Extracción de MFCCs (Mel-Frequency Cepstral Coefficients), basados en bancos de filtros aplicados al espectrograma.

Síntesis y Modificación de Audio

• Time-Stretching & Pitch-Shifting (e.g., Phase Vocoder).
• Reducción de Ruido: Filtrado en el dominio tiempo-frecuencia (e.g., Wiener Filtering).

Análisis de Instrumentos Musicales

• Identificación de parciales armónicos y transitorios.

Limitaciones y Alternativas

Limitaciones de la STFT

• Compromiso tiempo-frecuencia: No puede tener alta resolución en ambos dominios simultáneamente.
• Efecto de «Smearing»: Debido a la convolución con la ventana.

Métodos Alternativos

• Transformada Wavelet: Mejor resolución temporal para altas frecuencias.
• Análisis de Componentes Espectrales (PCA/ICA): Para señales complejas.
• Distribución de Wigner-Ville: Mayor precisión, pero con interferencias cruzadas.

Conclusiones

El análisis de Fourier en el dominio tiempo-frecuencia (STFT + Espectrograma) es una técnica poderosa para el procesamiento de audio, permitiendo:

• Visualizar la evolución frecuencial de una señal.
• Extraer características para machine learning.
• Modificar y sintetizar sonidos.

Sin embargo, su efectividad depende de una selección adecuada de parámetros (ventana, solapamiento, tamaño de FFT). Para aplicaciones avanzadas, pueden explorarse métodos como wavelets o modelos basados en redes neuronales.

Referencias

• Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing.
• Smith, J. O. (2007). Spectral Audio Signal Processing.
• Mallat, S. (2008). A Wavelet Tour of Signal Processing.